Impact and Fracture Mechanics Assessment of a Fused Silica Window
Analysis
Objective
Determine the survival probability of a fused silica window subjected to a large particle impact event within a hypersonic wind tunnel using numerical methods (LS-DYNA) and fracture mechanics theories for brittle solids. If damage is predicted, provide an assessment of the windows’ service life under repetitive pressure cycling of 14 psi.
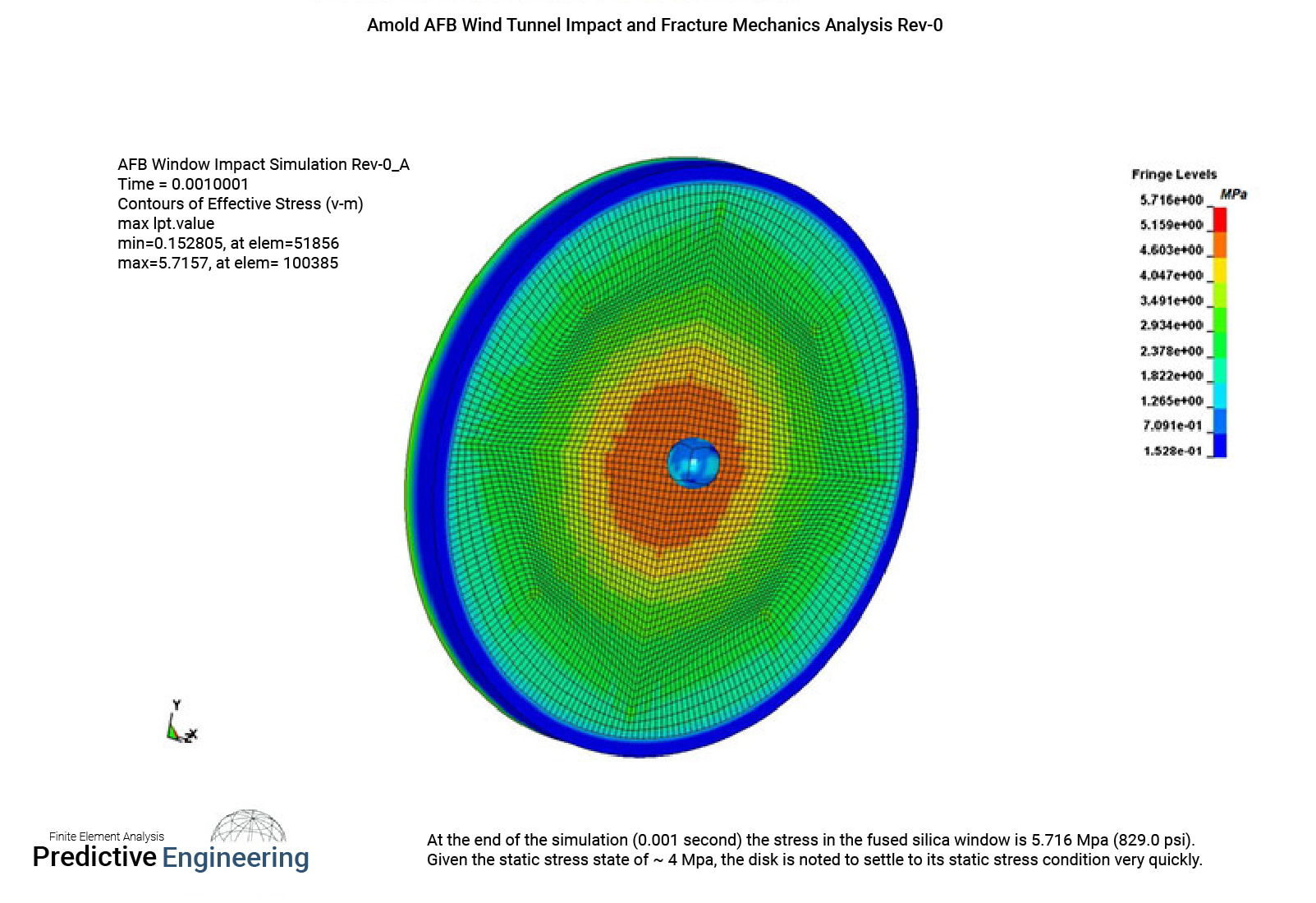
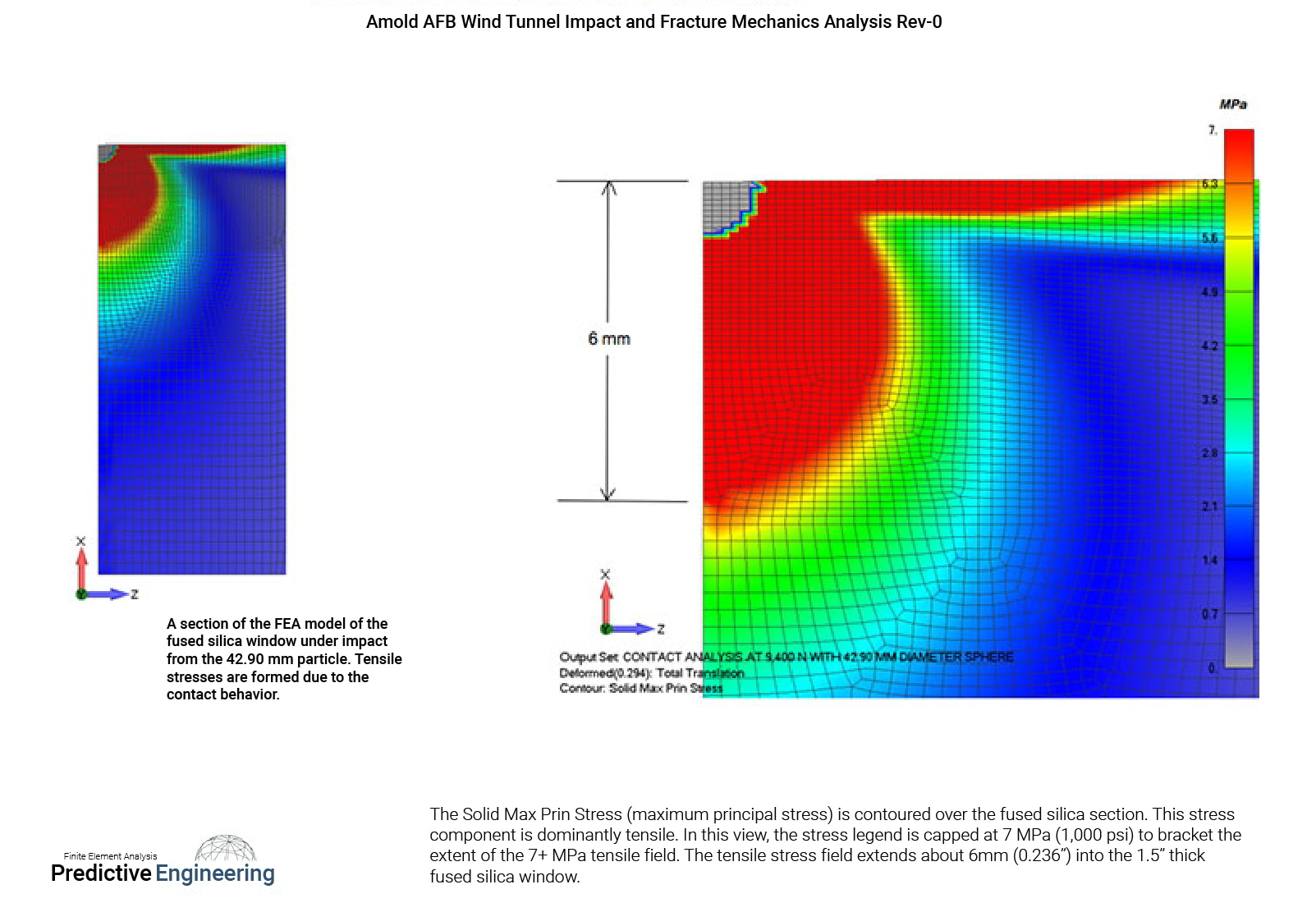
A finite element (FE) solid model of a 18” diameter, 1.5” thick disk was constructed based on information provided by the engineering team at Arnolds AFB (see Appendix). The FE model idealized a fused silica window that was potted into a steel frame using Ultracal 60 cement. The window is subjected to a differential pressure of 14 psi during hypersonic wind tunnel operation. This pressure tends to bow the window outward into the wind tunnel (internal side).
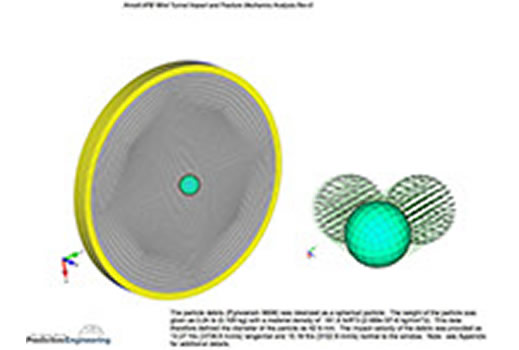
It is hypothesized that there exists a potential, during a specific wind tunnel test, for large particle debris (Pyroceram) to impact the window at
high velocities (12.27 ft/s tangential and 10.18 ft/s normal to the window). A nominal particle size was determined (see Appendix) and idealized
as a sphere with a diameter of 42.90 mm.
Mechanical property data for fused silica and Pyroceram 9606 is presented in the Appendix. It should also be noted that the mechanical
properties for fused silica are similar at 25 and 176C. Data for Pyroceram 9606 at 176 C was not available but is believed to follow a similar trend
as that for fused silica.
The analysis approach consists of model validation, impact simulation and interpretation of the results using fracture mechanics for brittle solids.
Auxiliary static stress models are also used to provide additional substantiation of the fracture mechanics predictions.
A side study that may be of interest to the readers is our work that we have done with Deep Ocean Engineering and Research (DOER) on glass mechanics as the structural hull for the world's first all-ocean deep-diving submarine (click here to download article). This research background article explores some of the challenges faced with glass hydrospheres and talks about how fracture mechanics of glass can be leverage for the safe design of a glass pressure hull.
PDF Download